基於齒輪測量中心圓弧圓柱蝸杆齒廓測量方法的研究

2019-12-24    click: 5981

  摘要：圓弧圓柱蝸杆傳動在工業自動化發展中具有重要地位，為確保使用過程中的穩定性和可靠性，必須對蝸杆的（de）精度進行檢測和分析，所以對（duì）圓弧圓柱蝸杆的各項誤差測量也是目前行業研究的重點與難點。根（gēn）據國標要求，圓弧圓柱蝸（wō）杆測量項目主（zhǔ）要包括齒（chǐ）廓、螺旋線（xiàn）和齒距三項，其中螺旋線與齒距測量相對簡單。本文（wén）重點討論圓弧圓（yuán）柱蝸杆軸截麵齒廓的（de）測量，基於（yú）圓弧圓柱（zhù）蝸杆軸截麵齒廓成型（xíng）原理（lǐ），建立蝸杆軸截麵（miàn）齒廓方程，在CNC齒輪測量中心上采用樣（yàng）條插補運動實現對圓弧圓柱（zhù）蝸杆軸截麵齒廓的測量，並對其采（cǎi）集誤差數據進行分離與（yǔ）補償（cháng），成功（gōng）實現（xiàn）了（le）對（duì）圓弧圓柱蝸杆軸截（jié）麵齒廓的測量，進一步提高了測（cè）量結（jié）果的準確度和精度（dù）。

  關鍵字：圓弧（hú）圓柱蝸杆；CNC齒輪測量中心；齒廓測量（liàng）；

0．引言

  圓弧圓柱蝸杆是一種非直紋麵圓（yuán）柱蝸杆，其（qí）齒麵一般為圓弧形凹麵。按照加工原理不同可分為圓環麵包絡圓柱蝸杆（ZC1）、圓環麵圓（yuán）柱蝸杆（ZC2）和軸向圓弧齒圓柱蝸杆（ZC3）三種類型[1]。經過理論分析，實驗研（yán）究以及在工業（yè）上的使用證明，在相同條件下，與普通圓柱蝸杆相比（bǐ），圓弧（hú）圓柱蝸杆具有承載能力大，齧合性能好，接觸麵積大，傳動效率高，結構緊湊，使用（yòng）壽命長等優（yōu）點，廣泛應（yīng）用於（yú）冶金、機械和（hé）化工等行業的重載設備中，這種以線共扼為齧合特征的蝸杆傳動對製造和安裝誤差及（jí）熱處理變形等較為敏感，由於誤差的影（yǐng）響，齒麵容易發生邊（biān）緣接觸（chù），常常導（dǎo）致蝸輪副的（de）早期損傷（shāng）和實效破壞[2]。因而對圓弧圓柱蝸杆的齒廓測（cè）量至關重要，要求（qiú）在加工過程中對誤差進（jìn）行控製，嚴格控製圓弧圓柱（zhù）蝸杆的齒廓誤差（chà），提高圓弧圓柱蝸杆的製造精度。

  圓弧圓柱蝸杆測量是（shì）目前行業麵臨的一個新的技術問（wèn）題。圓弧圓柱蝸杆測量主要包括齒廓，螺旋線以及齒距三個測量項目，一般（bān）螺旋線與齒距的測量相對簡單容易，針對齒廓測量，由於圓弧圓柱蝸杆（gǎn）加工原理的不同，其（qí）蝸杆（gǎn）軸（zhóu）截麵齒廓曲線也不同（tóng），既而蝸（wō）杆的軸截麵齒廓表達式也不同，較為（wéi）複雜。為解決圓弧圓柱蝸杆的齒（chǐ）廓（kuò）測量，哈爾（ěr）濱青青草网站測量儀（yí）器有限公司與北京工業大學精密工（gōng）程研究所合作（zuò），共同研究圓弧（hú）圓柱蝸杆的軸截麵齒廓成型原理，建立圓弧圓柱蝸（wō）杆（gǎn）軸截麵齒廓測量的數學模型（xíng），進一步實現圓弧（hú）圓柱蝸杆軸截麵齒廓測量，由於圓弧圓（yuán）柱蝸杆軸截（jié）麵齒廓（kuò）為（wéi）圓弧形（xíng）凹廓，所以在測量過程中測球與齒廓（kuò）接觸點（diǎn）的法矢不斷變化，存（cún）在測頭半徑補償問題。本文提出（chū）一種基於CNC齒輪（lún）測量中心圓弧圓柱（zhù）蝸杆軸（zhóu）截麵齒廓的測量方案，並重點討論相應誤差處理方法及測頭補償方法。

1．圓弧圓柱蝸杆軸截麵齒廓方程建立

1.1圓環麵包絡（luò）圓柱蝸杆（ZC1）

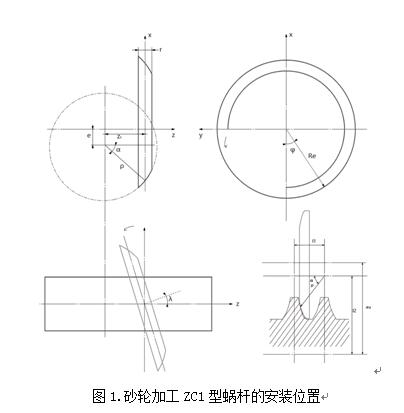
  圓環麵包絡圓柱蝸杆齒麵是由圓環麵（軸（zhóu）截麵為圓弧的砂輪）包（bāo）絡形（xíng）成的，磨削時，蝸（wō）杆軸（zhóu）線與砂輪軸線的軸交角等於蝸杆分度圓柱導程角，該兩（liǎng）軸線（xiàn）的公垂線通過蝸杆某一位置（依實際情況，單麵砂輪為齒廓分度圓處，雙麵砂輪為蝸杆齒（chǐ）槽中點）[3~4]，砂輪表（biǎo）麵與蝸杆齒麵的瞬時接觸線（xiàn）是一條固定的（de）空間曲線，由齒廓形成原理可知（如圖1所示），經（jīng）過建立坐標方程（chéng）推導出軸截麵齒廓方程為：






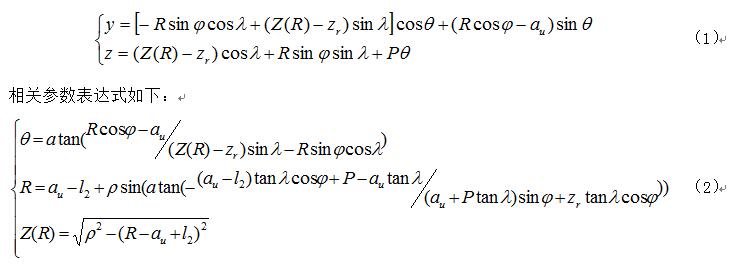
由表達式（2）可（kě）計算（suàn）出相應參（cān）數 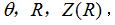   ，進一步代入表達（dá）式（1）中（zhōng）可求解圓環麵包絡圓柱蝸杆（ZC1）的軸截麵齒廓坐標。

式中：y,z為軸截麵齒（chǐ）廓坐標；

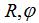       分別為齒廓上點與加工砂（shā）輪接觸時，與（yǔ）加工砂（shā）輪軸（zhóu）線距（jù）離和回轉（zhuǎn）角；

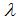   為蝸杆導程角；

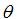   為相對初始位置蝸杆轉角；

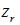   為砂輪軸截麵圓弧圓心到蝸杆與砂輪中垂（chuí）線的距離，對於單麵砂（shā）輪（lún）來說  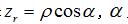   ,為砂（shā）輪分（fèn）度圓點曲率半徑與砂輪軸（zhóu）線夾角（jiǎo），對於雙麵砂輪來說，  由砂輪寬度計算，公垂線在齒槽中點；

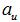   為加工時砂輪軸線與蝸（wō）杆軸線最短距離；

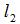   為砂輪對蝸杆軸線偏轉之前砂輪軸（zhóu）截麵圓心與蝸杆（gǎn）軸最（zuì）短（duǎn）距離；

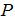   為螺旋參數；

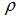   為砂輪軸截麵圓弧曲率半徑（jìng）。






1.2圓環麵圓柱蝸杆（ZC2）

  與圓環麵包絡圓柱蝸杆（ZC1）都是磨削蝸杆，隻（zhī）是形成原理不同，安裝時，圓環麵圓柱蝸杆（ZC2）是通過調整（zhěng）砂輪與蝸杆軸交錯角，使兩軸公垂線通過砂輪齒廓的（de）曲率中心，這就（jiù）意味著砂輪與蝸（wō）杆的瞬時接（jiē）觸線變為與砂（shā）輪軸截麵（miàn）的圓弧重合的平麵曲線。由齒廓形成原理可知（如圖2所示），經過建立坐標方程推導出（chū）軸截麵齒廓方程（chéng）為：









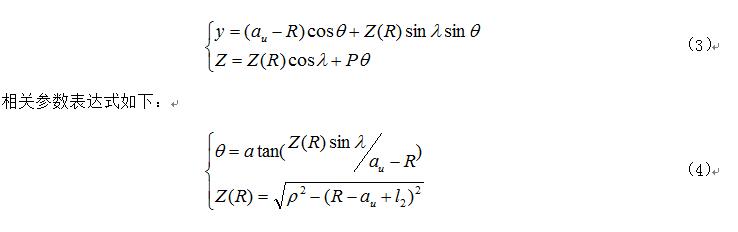
由表達式（4）可計（jì）算出相應參數（shù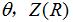）    ，進一步代入表達（dá）式（3）中可求（qiú）解圓環麵圓柱蝸杆（ZC2）的軸截麵齒廓坐標。

式中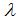： 為砂輪軸線與蝸杆軸線交錯角，由  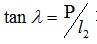  求出（chū）；

      其（qí）餘參數意義同圓環麵包絡圓柱蝸杆（ZC1）齒廓方程參數。






1.3軸向圓弧圓柱蝸杆（ZC3）

  軸向圓弧圓柱（zhù）蝸杆（ZC3）加工原理（lǐ）相對簡單，是由圓弧刃口的車刀車削而成，加工（gōng）方式與（yǔ）阿基（jī）米（mǐ）德蝸杆類似，將車刀（dāo）圓弧刃口置於蝸杆軸截麵做相對螺旋運動，故軸向圓弧圓柱蝸杆（ZC3）軸截麵齒廓（kuò）為一（yī）段圓弧。由齒廓形成原（yuán）理可知（如圖3所示），軸截麵齒廓方程較為簡單，以y軸經過軸截麵齒廓中點建立坐標方（fāng）程推導出軸截麵（miàn）齒廓方程為：






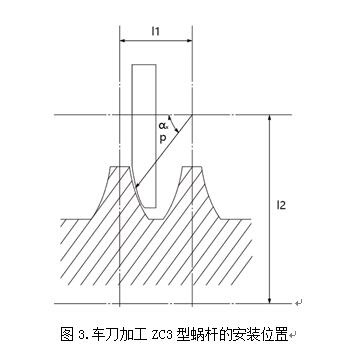
2.圓弧圓柱蝸杆軸截麵齒廓測量及誤（wù）差數據處理

2.1求（qiú）解圓弧圓柱蝸杆軸截麵（miàn）齒廓坐標（biāo）規劃測量軌跡

  基於齒輪測量中心，求解圓弧圓柱蝸杆軸截麵（miàn）齒廓坐標 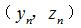  ，控製儀器Y軸和Z軸聯動實現蝸杆軸截麵（miàn）齒廓掃描測（cè）量（liàng），測頭的（de）微變化量反映齒麵加工誤差，如圖4所示。鑒於圓（yuán）環麵（miàn）包絡圓（yuán）柱蝸杆（ZC1）、圓環麵圓柱蝸杆（ZC2）軸截麵齒廓方程（chéng）均為超越（yuè）方程，其處理方式為根據變參數  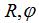 離散得到一組足夠多的等間隔軸（zhóu）截（jié）麵齒廓坐標點  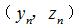 ，軸向（xiàng）圓弧圓柱蝸杆（ZC3）可通過（guò）軸截麵齒廓方程直接獲取一組等（děng）間隔軸截麵齒廓坐標點  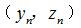 。如果使用球形測頭對這三種蝸杆的軸截麵（miàn）齒廓（kuò）進行測量，通過齒輪測量中（zhōng）心讀出的數（shù）據為（wéi）測（cè）球中（zhōng）心的位置坐標，而不是測球球（qiú）形表麵和工件實際接觸點的位置坐標，這（zhè）樣獲取的坐標值與理論接觸點坐標計算比較，得到的結果會有（yǒu）一定（dìng）的（de）誤差。為了便於測量和（hé）得到正確的測量結果，應對被測點進行測球（qiú）半徑補（bǔ）償。因此需（xū）要將（jiāng）求解的蝸杆軸截麵齒廓坐標（biāo）點  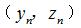 轉換到與之（zhī）對（duì）應的測球軌跡坐標點，這樣才能保證測球與工件接觸點與理論齒廓坐（zuò）標點一致，避開了（le）測球半徑導致接觸點變化給測量結果（guǒ）帶來的影響。即（jí）根據求（qiú）解蝸杆軸截麵齒廓坐標點   ，找到測球中心與對應接（jiē）觸點的坐標之間（jiān）的轉換關係，便（biàn）可（kě）獲得測球測量（liàng）軌（guǐ）跡的坐標。

  問題（tí）的難（nán）點在於如何求取實際接觸（chù）點的法線方向，如果被測曲麵的形狀已知，且（qiě）可以用一定形（xíng）式（shì）的解析函數表示，那麽就可以（yǐ）用解析的方法求（qiú）出曲（qǔ）麵每個點的法線方向，按照求得的法線方向確定與理論齒廓相接觸（chù）的對應測球球心軌跡坐標，但是圓弧圓柱蝸（wō）杆的軸（zhóu）截麵齒廓方程為（wéi）超越方程，直接通（tōng）過解析函數求（qiú）出（chū）每個點的法線方向比較複雜。可以通過微平麵法求解測球與工件接觸點的法矢，進一步求得與理論軸截麵（miàn）齒廓實際接觸點相對應的測球測量軌跡坐標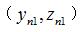   



   由於這三種蝸杆軸（zhóu）截麵齒廓均為複雜曲線，為實現實際測（cè）量軌（guǐ）跡接近理（lǐ）論曲線，通過上述軸截麵齒廓方程離散獲得（dé）一組足夠多的等（děng）間隔采樣點，當離散點的最（zuì）大間隔均低於測量精（jīng）度的0.1倍時，就可認為離散出的點列等效於理論齒廓。本文采用GTS係（xì）列運動控製器中的PVT運動模式，該運動模式能實現單次走1024個點位且運動平滑。實際運動過程中依據采樣點位置選取包括采樣點在內（nèi）的略（luè）小於1024個的點，實現采樣點位置的準確測量。 



2.2誤差數據處理  

  在齒輪測量中心上對圓弧圓柱蝸杆進行測量時，把被測工件實際幾何形狀的坐標測（cè）量值與計算機所計算的（de）理論坐標值進行比較，得到被測工件測量的實際偏差。由（yóu）於在（zài）測量過程中，受到控製精度和外部環境的（de）影響，實際（jì）Y軸和Z軸存在運動誤差，影響測量結果（guǒ）的精度，所以需要進行運動誤差補償。

（1）誤差數據的獲取（qǔ）

  按照上述規劃測（cè）量（liàng）路徑對其軸截麵齒廓進（jìn）行測量，測球與被（bèi）測件實際接觸點（diǎn）就是理（lǐ）論齒廓（kuò）坐標（biāo）點，由於蝸杆存在加工誤差，在測量過程中，測頭在Z軸方向的變化量即為齒麵加工誤（wù）差。實際被測點如果和理論坐（zuò）標點完全重合，測頭變化量為零（líng），即齒麵誤差為零，但是由於齒麵存在加工誤差，測頭會有微變化量 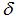   ，測球與工件（jiàn）實際接觸（chù）點假想在半徑無窮大的圓上，那麽測頭（tóu）的變化量  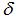 等效於實際齒麵加工誤差，對於測微小變化（10μm以內（nèi））該等效過程產生（shēng）的偏差可忽略。

（2）運動誤（wù）差補償

  無（wú）運動補償齒廓測量（liàng）曲線波動較為明顯，這是因為在測量過程中受到運動誤差的影響，測頭微（wēi）變化量並不能真實反映實際齒麵誤差，所以需要進行運動誤差補償（cháng）。即通過實時采集（jí）Y軸（zhóu）和（hé）Z軸數據，根據（jù）采集（jí）當前數據計算由於Y軸、Z軸運動誤差，帶來Z軸方向上的誤差分別為 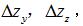   ，即蝸杆軸截麵實際齒廓誤差  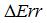   為：






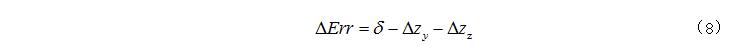
3.測量（liàng）實驗

  測量實驗采用軸向模數為4.0，法向（xiàng）壓力角為20°，導程角為11.2188°及砂輪半徑為240的ZC2型蝸（wō）杆。在齒輪測量中心上對其進行軸截（jié）麵齒廓的（de）測量，測（cè）量結果報告單如下。



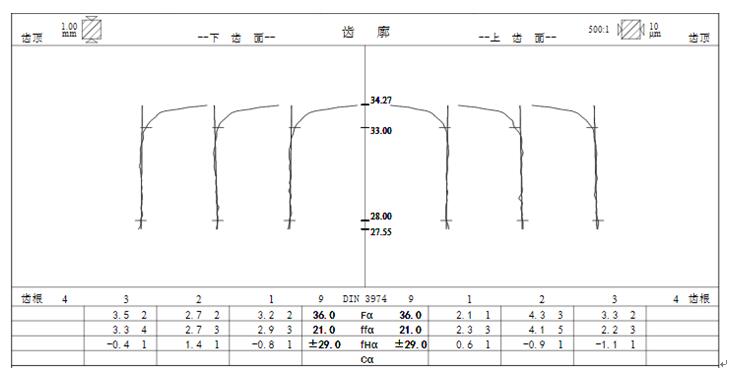
 穩定性實驗是對同一ZC1型（xíng）蝸杆的同一齒廓（以第一齒右齒麵為例）進（jìn）行多次（5次（cì））測量，將結（jié）果進行比對。結果如表（biǎo）1。



  由表1中測量結果可以得出ZC1型蝸杆軸截麵齒廓測量方法可行，同理可測ZC2型和ZC3型（xíng）蝸杆，可以實（shí）現三（sān）種形式蝸杆軸截麵齒廓（kuò）的（de）測量，並且測（cè）量結果穩定，精度和準確度很高。

4.總結

  本文提出了（le）一種圓弧圓柱蝸杆軸截麵齒廓測量方法（fǎ）及誤（wù）差處理方（fāng）法，成功實現了圓弧圓柱蝸杆軸截麵齒廓的測量，並進一步（bù）提高了圓弧圓柱蝸杆軸（zhóu）截麵齒廓測量的準確度和精（jīng）度。通過測量結果對蝸杆軸截麵齒廓誤差進行分析，並由此調整（zhěng）加工時蝸杆的安裝位置和加工圓（yuán）弧圓柱蝸杆的加工參數，提高圓弧圓柱蝸杆的（de）加工精度。經過（guò）實際（jì）測試表明，該測量方法正確可行，測量結果穩定、準確。




參考（kǎo）文獻：

[1]石照耀，葉勇，丁毅，張勇（yǒng），薑誌強.圓弧圓柱蝸杆的齒廓（kuò）測量（liàng）與參數（shù）反求[J].工具（jù）技（jì）術,1999(01):33-36.

[2]石萬凱，秦大同，田川（chuān）寶.提高（gāo）ZC1蝸杆（gǎn）製造精度的（de）研究[J].重慶（qìng）大學學報(自然（rán）科學版),1998(05):63-69.

[3]嚴以（yǐ）銳.圓弧齒圓柱蝸杆齒（chǐ）形（xíng）的測量[J].機械工人.冷加工,1991(11):41-42.

[4]封（fēng）增祺.圓弧圓柱蝸杆齒形計算[J].機械,1989(06):14-15.